02.02 How can I create a model of something that is very large?
Abstract Reasoning

02.02 How can I create a model of something that is very large?

 , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,

(introduction = 3 minutes reading and a 7 minute video)

To Scale: The Solar System from Wylie Overstreet on Vimeo.

The distances between the planets are very large and ever changing as they move around the sun. There are a few ways of expressing very large numbers. One google can be written as:

  1. 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
  2. 10 x 1099
  3. 10100

None of the distances between planets are convenient numbers like one google and therefore, the distances need to be referred to using using scientific notation, like #2 above, which is an extension of using exponents like the #3 above. The first way of referring to 1 google as 1 followed by 100 zeros is not very helpful as your eyes just get lost in the quantity of digits, so similarly, the distances would be equally annoying: the distance from the earth to the sun on the day this post was written was approximately 148.56 million km, or 148 560 000 km or 148 560 000 000 metres or 148 560 000 000 000 cm or 1.4856 x 108 km.

Watch the online video featured on this article [web page] (and above) to see how an accurate model of the solar system was made.

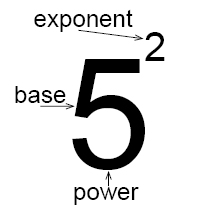
Review of exponents and exponent laws

Exponents are a condensed way of expressing a number multiplied by itself. The number (or variable) multiplied by itself is called the expanded form.

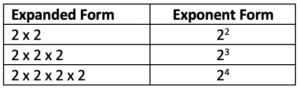
Exponent and Expanded Form

02.02.01 What do I remember about exponents?
exponent base and power(approximately 20 minute review activity)
This activity should have only one new to you idea (1c and 2c).

 

(Re)Discovering Exponents Hint 1
  • compare the numerical values of 22 and 2-2 as well as 23 and 2-3
  • compare other numerical values of bases that have the same positive and negative exponent

 

(Re)Discovering Exponents Hint 2

 

(Re)Discovering Exponents Key

 

 

02.02.02 What do I remember about exponent properties/laws/rules?
rules(approximately 30 minute review activity or reading)

 

02.02.03 Am I confident using exponents in calculating money matters?
(approximately 5 minutes total reading, two activities 20 to 30 minutes each plus time to self-assess against provided Keys and Rubrics)

$1000 a week for life or a million now?

lottery balls fallingPhoto by dylan nolte on Unsplash

Your parents have just won the $1000 a week for the rest of your life jackpot. They have the choice to take the $1000 a week or a 1 million dollar payout immediately. Which should they take? The compound interest rate (where you get paid the interest monthly and then earn interest on that interest the next month) is A = P(1 + r/n)nt where A is the amount at the end of a portion of time, P is the amount invested, r is the annual interest rate in decimals (3% would be 0.03), n is the number of compounding periods per t (so monthly would be 12),  and t is the time involved in years.

  1. Calculate the amount they would have in 10 years if they didn’t touch any of the money and earned 3.875% interest a year. (Check your math using this online calculator).
  2. How much interest would there have been over 10 years?
  3. Can you see how the $1000 a week would have been calculated as an option?
  4. If they had been taking out the interest every week, how much would they be removing?
  5. Check your amount against current interest rates on safe investments like a fixed annuity or savings account.  Check your calculations so far (see hint below)
  6. How much taxes would they have to pay on $1000 a week or the 1 million payout? See this website to check on Canadian laws on lottery winnings.
  7. How many debts would your family pay off with 1 million (consider mortgage, car loans, or purchases that could be made to make life easier on a day to day level).
  8. Include a small portion, less than 5% to celebrate by taking a trip and/or buying new furniture and/or appliances and/or vehicles.
  9. Based on your calculations and family situation, advise your parents on what you think their choice should be.
Key to #1-5
  1. Total investment after 10 years at 3.875% interest:
    • P(1 + r/n)nt
    • 1 000 000 (1 + 0.03875/12)10•12
    • 1 000 000(1 + 0.0032291667)120
    • 1 000 000(1.0032291667)120
    • 1 000 000(1.472 373 45)
    • $ 1,472,373.45
    • where you choose to round can change the amount significantly. If you used 1.003 before applying the exponent, your final answer would be over $10,000 more!
  2. Interest over 10 years if no money was removed from the account $474, 373.45
  3. How was ‘$1000 a week for life’ calculated? Interest divided by 10 years of 52 weeks is $474, 373.45 / 520 = $912 a month which is approximately $1000. Note, you could also calculate by dividing by 521.4 as the number of weeks in a year is not a whole number.
  4. If the rate is still 3.875, then the calculation would be Principal • rate /52.14 to calculate the amount removable by week. P•r/52.14= $743.19 per week. Most banks would not calculate interest weekly, though, so the calculation should be done monthly (P•r/12). P•r/12= $3229.17 per month.
  5. At the time of this post, Guaranteed Income Certificates (GIC) are earning only between 0.4 % and 2% a year for GICs of a minimum investment of $1000 with an annual compound interest rate and not cashable early.

 

Elements for considering #7-9
Your home

  • Is there a mortgage on your house?
  • The size, suitability, and area your house is in and whether it would be better to move
  • Whether the house you might move to would be affordable if you spent most of your million dollar payout on it
  • The pleasure you would get out of a new house or upgrades to your house
  • New appliances
  • Furniture changes to fill a new house or to make yours more comfortable
  • How long everyone currently in the house would be living in that house

Family Debts

  • How much does your family owe on credit cards?
  • How much does your family owe for vehicles?
  • How old are your vehicles and do they need replacement soon?
  • Would you family like another vehicle or a recreational vehicle?

Income

  • Does the current family income cover all expenses?
  • How much will further schooling cost for the young people in your home?
  • Does a parent want to stop working?
  • How much taxes are charged for winnings from a lottery? Does the 1 million dollar payout have a larger tax requirement than $1000 a year?

Age

  • How old are your parents? Will the $1000 a month be a way for them to accumulate money?

 

Rubric to assess #1-9
  • Limited – You had the amounts for #1-3 correct. You considered few of the elements for #7 – 9 listed above.
  • Adequate – You had the amounts for #1-4 correct. You considered some of the elements for #7 – 9 listed above.
  • Substantial – You had the amounts for #1-4 correct. You considered many of the elements for #7 – 9 listed above.
  • Excellent – You had the amounts for #1-4 correct. You considered most of the elements for #7 – 9 listed above.

Consider this 18 year-old’s choice (website).

 

Chain letters!

Money from different countriesPhoto by John McArthur on Unsplash

You have received an email from a friend. It has a list of 8 names and addresses. It tells you to send $5 to the name at the top of this list. Then you are to delete the name and address you sent money to and add your own name and address at the bottom of the list. Then send the email to 5 new friends.

1. If that process goes as planned, how much money would you expect to receive?

2. What could possibly go wrong? Explain your answer clearly.

Research ‘ponzi’ or ‘pyramid’ schemes. Is this legal? Why or why not?

Key to Chain letters
  • Limited – You calculated #1 as 5 to any power greater than 2. You considered that not everyone contacted would send the money or send the email on to others or the email might go to Spam.
  • Adequate – You calculated #1 as $58 or $390625. You considered that not everyone contacted would send the money and/or send the email on to others that not everyone contacted would send the money and/or send the email on to others and/or it is a scam/illegal because: it gives people an unrealistic expectation of what they will receive and/or it takes people’s money and they may not receive any (at least 2).
  • Substantial – You calculated #1 as $59 or $1953125 (or rounded it to 2 million dollars). You considered that not everyone contacted would send the money and/or send the email on to others that not everyone contacted would send the money and/or send the email on to others and/or it is a scam/illegal because: it gives people an unrealistic expectation of what they will receive and/or it takes people’s money and they may not receive any (at least 3).
  • Excellent – You calculated #1 as $59 or $1953125 (or rounded it to 2 million dollars). You considered that not everyone contacted would send the money and/or send the email on to others that not everyone contacted would send the money and/or send the email on to others and/or it is a scam/illegal because: it gives people an unrealistic expectation of what they will receive and/or it takes people’s money and they may not receive any (at least 4).

This task is from the Mathematics Assessment Resource Service [web page].

 

Exponent Review Games
(an hour to a few hours, depending on your comfort manipulating exponents)
To ensure you can apply exponents accurately in any situation, you can review exponent laws by:

Remember, a negative exponent does not mean you have a negative number. A negative exponent on a whole number or variable just means you have a number between 0 and 1, a fraction. The negative exponent translates to a positive exponent if you switch the base to its reciprocal.

Alternatively, use the Math Aids [web page] worksheets. Choose whether you want to practice both positive and negative exponents or just positive exponents. Be sure to click the button for an answer key.

  • Exponents with Multiplication
  • Exponents with Division
  • Exponents with Multiplication and Division
  • Powers of Products
  • Powers of Quotients
  • Powers of Products and Quotients
  • Operations with Exponents

 

02.02.04 How are old items dated?
(approximately 1 minute reading, 10 minutes solving, suggested hour practicing with fractional exponents)
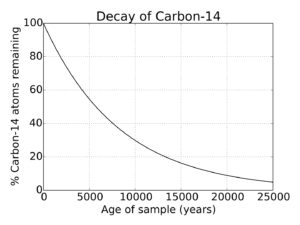
Radioactive decay of Carbon graph
Most living things are made from Carbon-12. Carbon-14 was discovered in 1940 (website article about Carbon-14). Carbon-14 exists in extremely low levels in the tissues of recently deceased animals and plants: about one in a trillion of their carbon atoms are carbon-14. By measuring the radioactivity of the Carbon-14 in something deceased, its date of death can be calculated.  The equation for radioactive decay is:

  • A=A0•(½)t/h
  • A0 is the original amount of a radioactive substance
  • A is the final amount
  • h is the half life of the substance
  • t is the time

If the half life of Carbon-14 is about 5730 years and a fossil currently contains 2 grams of Carbon-14, and the estimation is that it would have originally had 64 grams of Carbon-14, how old is the fossil?

Investigation of relationship between fractional exponents and radicals
(approximately 1 minute reading and a thirty minute investigation)

 

Practice using fractional exponents and radicals
(approximately 1 minute reading and 20-30 minutes of practice)

 

Investigation about basic logarithms that can help you solve the problem
Logs (approximately 20 minute investigation)
Logarithms sound difficult but actually have a simple relationship. Before starting this investigation, look up how to punch in a logarithm on your calculator. On our calculators, “log” (without any base) is taken to mean “log base 10“. So, for example “log 7” means “log107“, which should show up on your calculator as 0.845098 . . .

 

Hint (substituting values into the question) to solve how old the fossil is
2 = 64•(½)t/5730

 

Key to how old the fossil is
2 = 64•(½)t/57302/64 = (½)t/57301/32 = (½)t/5730  Adequate Level(½)5 = (½)t/5730  Substantial Level5 = t/5730  Excellent Levelt = 5•5730t = 28 650 years old

 

02.02.05 How do I make a model of the solar system?
Model of Solar System (orrery)(approximately 1 minute reading and an hour on review if needed, then a twenty minute activity)
You need to be comfortable with Scientific Notation for this task. Choose your method(s) to practice for accuracy. Online practice can be done through

If you need more instruction:

You can use the Math Aids [web page] worksheets. Be sure to click the button for an answer key.

    • Writing Numbers in Scientific Notation
    • Operations with Scientific Notation

You have been asked to make a solar system model for science class. Utilizing scientific notation, you do the required preliminary assignment: Solar System Model Google Doc or download the Solar System Model pdf. Check your work against the Solar System Model KEY Google Doc or download the Solar System Model KEY pdf. (This assignment is based on an assignment found at StudyLib.)

Suggested online video: If the Moon were only one pixel

For Teachers: