(approximately 8 minutes reading, a 10 minute activity and a 20 minute slideshow/activity)
(approximately 8 minutes reading, a 10 minute activity and a 20 minute slideshow/activity)
Photo by Christiann Koepke on Unsplash
Read this online article on how credit card interest is calculated and, while following through the calculations provided, work through the approximate calculation using an APR of 20.24% and the 25 days of charges on the following two images. Then check your math against this online article on credit card interest calculations.
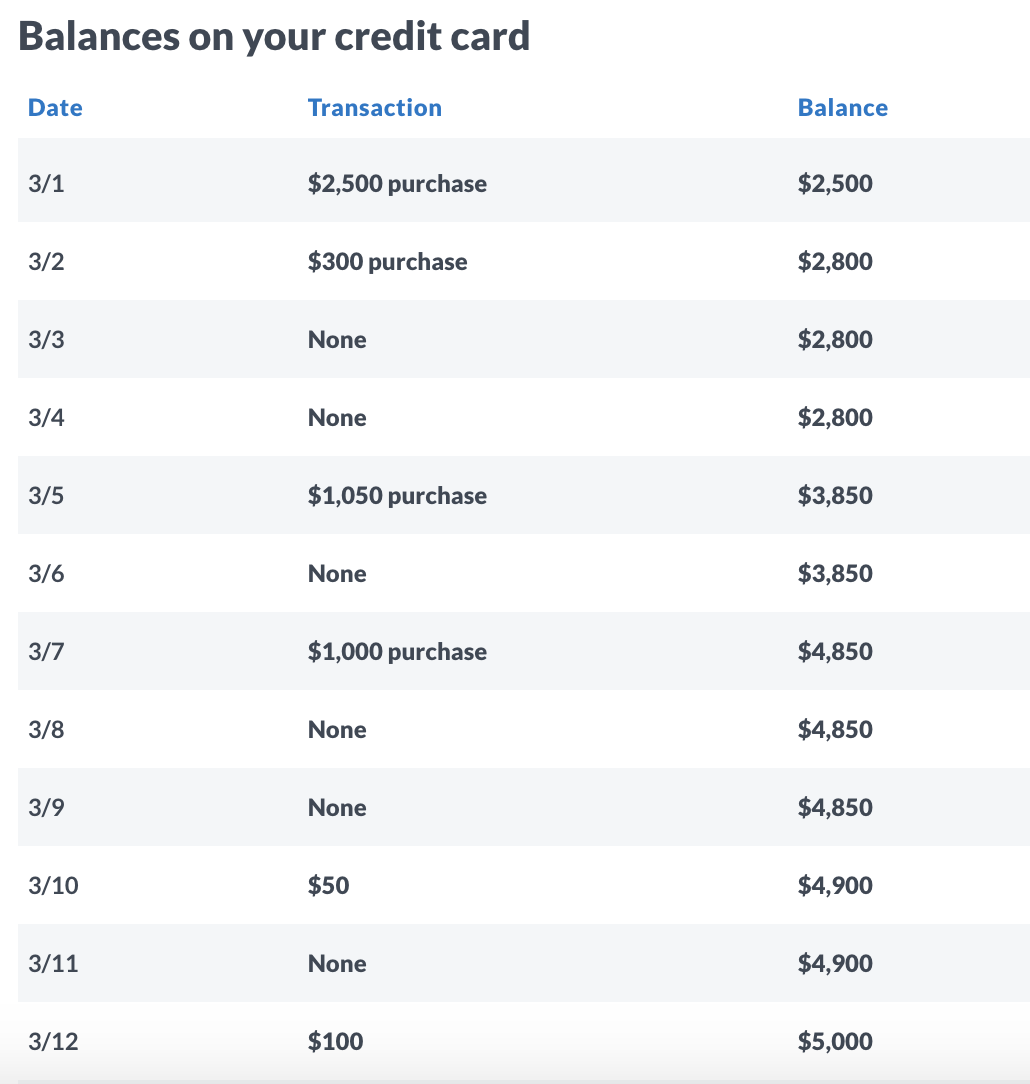

The real calculation, as you have read, is more involved. If you were charging to your credit card the same amount daily your increased balance would be an arithmetic sequence and easy to calculate. The interest calculated on the daily basis would be a geometric sequence.
Read through this online presentation on other real-life applications of arithmetic and geometric sequences. Do the math examples as you go.
02.05.01 What investing plan is best?
 (approximately 2 minutes reading, an hour reading and doing examples, and 20 minutes on the task)
(approximately 2 minutes reading, an hour reading and doing examples, and 20 minutes on the task)
Photo by Andre Taissin on Unsplash
Investing plans calculate interest on specific days. When planning how to invest your savings, you will want to compare plans based on not only the interest they provide, but whether they have a fixed interest rate for a specific time frame with a penalty for early withdrawal (like a bond) or whether the interest is variable with no penalty for withdrawals (like a savings account). To compare investing plans, you will need to know approximately how much you will save, how often you will deposit into the account, and what the interest rate is. This calculation is easy if you understand arithmetic sequences.To learn more about how to recognize arithmetic sequences and how to calculate for a particular number in an arithmetic sequence, read one of the following websites:
- Arithmetic sequences on the Math is Fun website (summing an arithmetic sequence or series isn’t required, but is easy and interesting though it looks complicated. Do the ‘Your Turn’ at the bottom.)
- Arithmetic sequences on the Math Planet website (includes a video)
- Arithmetic sequences, including recursive sequences on OpenText BC website.
If you look at an arithmetic sequence equation, it looks like a linear function, which you would have studied in previous math classes. The main difference between the two is an arithmetic sequence is discrete (has set values) whereas a linear function is continuous. Remember that height, weight and age are all considered continuous values, but number of people are discrete values (because you can’t have a portion of a person). If you want a more complete answer, you may choose to read this website comparing arithmetic sequences and linear functions.
An arithmetic sequence has the general rule:
tn=a+(n-1)d where tn is the nth term, a is the first term, or t1, and d is the common difference (the difference between each of the terms in the arithmetic sequence).
As a simple starting question, consider a $750 investment which, after a year in a savings account, was worth $783.75, after two years was worth $817.50, after three years $851.25 and after 4 years $885. What would be:
- the annual interest rate?
- the general term for the balance at the end of the nth year?
- the balance at the end of the 15th year?
Check your answers against the example of page 5-7 of this online textbook excerpt.
If you want, compare current interest rates on savings accounts, chequing accounts, and savings bonds and discuss with your parents which you should be using for your savings.
02.05.02 Is it better to lease or buy a car?
 Photo by Alan Flack on Unsplash
Photo by Alan Flack on Unsplash- Geometric sequences on the Math is Fun website
- Geometric sequences on the Math Planet website (includes a video)
- Geometric sequences, including recursive sequences on OpenText BC website.
For a clear comparison between geometric sequences and exponential growth (which we covered in 02.03), read through this online book and do the questions at the end. (approximately 10 minutes reading and 30 minutes of exercises)
Consider the difference between leasing and buying a car priced at $26,000. Compare a 3-year loan and a 3-year lease for this car. After 3 years, the car will be worth 50% of original value, or $13,000 — regardless of whether we lease or buy. Use a finance rate for both the loan and lease of 5.0% APR. Assume no down payment for either. How much will your monthly payment be for a loan? Remember when finding your formula, your monthly payment is decreasing your total amount, though you are also increasing the amount because of the interest.
Hint for 02.05.02 (the formula)
Read this online article to assess your math against. Don’t worry if you are off by a few cents as that is because of rounding. Considering whether you are planning to keep the car after 3 years and how much you expect to use it, is it better for you to lease or loan? You may want to read some of the other articles listed at the bottom of the article.
If you enjoy nth term rules (arithmetic and geometric sequences) as a form of puzzling, this website has visual patterns which can be puzzled into a mathematical equation to calculate the 43rd term (answers are provided for each, but not the mathematical equation).
2048 was a popular app [website] involving the doubling pattern.
For Teachers: